达人

家在深圳
11,045.2K话题 5,942.2K关注 67昨日发布

达人

11,045.2K话题 5,942.2K关注 67昨日发布

立即下载

热 浏览 10076评论 257
浏览 657评论 23

浏览 239评论 9
热 浏览 11087评论 94 #人生经历#

浏览 14评论 0 #生活情感#

浏览 8640评论 132
浏览 667评论 10
浏览 3959评论 68 #人际关系#

热 浏览 75776评论 272
浏览 381评论 2 #婆媳#
浏览 495评论 11 #婆媳#



浏览 2892评论 56 #生活情感#
浏览 2301评论 51
热 浏览 15472评论 124 #吐嘈#
浏览 2765评论 48
浏览 9583评论 68 #相亲#

热 浏览 13456评论 134
浏览 526评论 6

浏览 9160评论 82
浏览 1888评论 14


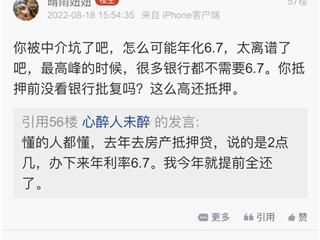
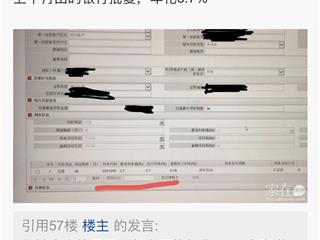
热 浏览 4900评论 339
浏览 219评论 11 #日常点滴 #
浏览 323评论 4 #日常点滴 #
浏览 233评论 2
浏览 5671评论 51 #相亲#
热 浏览 12224评论 104 #工作问题#
浏览 9667评论 49
浏览 858评论 17
浏览 4825评论 35 #工作问题#
浏览 157评论 3
浏览 378评论 0

浏览 7503评论 60



浏览 218评论 14
浏览 3680评论 30
浏览 5107评论 54
浏览 541评论 8
热 浏览 17895评论 155 #日常点滴 #

热 浏览 25450评论 147 #日常点滴 #
浏览 549评论 27 #日常点滴 #




浏览 3195评论 47 #恋爱#